Academic Project: Optimization of Mini-Max Algorithm using Alpha-Beta Pruning technique

Project By – Krishna Adatrao
Guidance & Evaluation: Prof. Dr. Selena He, Kennesaw State University

We have implemented the Connect4 game. Connect4 is a two-player board game with six rows and seven columns grid. Our bench-mark algorithm is Mini-Max Algorithm, and our optimal or proposed algorithm is Alpha-Beta Algorithm. Here, our implementation is to reduce the compilation time taken by Mini-Max Algorithm to make an optimal move. Subsequently, we proposed an Alpha-Beta pruning algorithm for better implementation of the connect4 game compared to Mini-Max. Though Alpha-Beta pruning is not a different technique, we found that the algorithm has a structural strategy to directly pick the optimal path and then optimal move in half of the time of mini-max. Further, we have justified our statements by calculating time complexity, space complexity, and accuracy for both algorithms according to the gathered data (compilation time data, space allocation data, and output data for both the algorithms). Furthermore, we plotted comparison graphs to illustrate the differences between the algorithms visually.

People intertwined with the games in ancient times, which became an essential part of human life for recreation and enthusiasm. Recently, the advancements of AI in the present world made outdoor games like cricket, hockey, tennis, etc., flexible to play virtually. Subsequently, we initiated AI collaboration with a small board game, connect4, mostly played in the Soviet Union. Our project is to create a connect-4 game between the user and AI. Accordingly, we implemented a mini-max algorithm (Benchmark Algorithm) as an AI for our project. The mini-max algorithm accuracy and precision in making an optimal move were phenomenal. However, the compilation time of mini-max is huge at higher depth values. The depth value is the height or level of the tree, while it is the difficulty factor in-game scenario. Our bench-mark algorithm investigated the problem is that going to deeper depth or adding more levels to a tree would probably make the mini-max algorithm high in time complexity. 

The progress here is to make an actual enhancement of the Mini-Max algorithm. Subsequently, we proposed Alpha-Beta Algorithm as AI to our program, which made an outstanding performance in predicting an optimal move in half of the compilation time of mini-max. Though both the algorithms provide almost the same solution and accuracy, alpha-beta gave the output quickly with less time complexity. Hence, alpha-beta pruning search can search twice as profoundly within the same time taken by mini-max. Moreover, mini-max’s highest depth value is 5 (depends on the CPU performance).

On the other hand, alpha-beta went to 8 depth value. Further, we implemented both algorithms to the connect4 game to illustrate the concept visually. The alpha-beta pruning technique is not an alternative to the mini-max algorithm. Possibly it’s something we layer on top of the mini-max. In conclusion, it does give an almost similar solution as mini-max. Nonetheless, all its work is to cut off many nodes to achieve the solution quickly.

We have chosen this project as challenging because while going deeper into the depth level in the mini-max algorithm, the AI has been taking a forever amount of time to reflect the output. Hence, our motive is to sustain the accuracy and reduce the time complexity while going to a deeper depth level. Therefore, we have been trying to make the optimal predictions in the higher depth levels with less time complexity and good efficiency. 

Here we observed a problem related to the compilation time taken by our bench-mark algorithm (mini-max algorithm), which is enormous. In board games, the time utilized by an AI to perform a move should be limited for a better user experience. Hence, we proposed an optimal adversarial search technique as an alpha-beta pruning algorithm that prunes the unnecessary portion in the tree. We justified our solution to the problem accordingly to the below assimilates provided for both the algorithms. 

Solution:

We can reduce the compilation time taken by the mini-max algorithm according to the direct pick of the optimal path carrying in the tree rather than analyzing the entire tree. However, we observed that the alpha-beta algorithm is perform the complete analysis of the tree to get the outcome of the optimal path but does not explore all the paths in the tree. So, we preferred the alpha-beta pruning algorithm, which eliminates the unnecessary branches of the tree while checking the tree. In this manner, alpha-beta pruning limits its search time. 

According to the game theory, mini max is a decision-making rule-based used in AI statistics. The fundamental of mini max is to perform on maximizing and minimizing player rules. For the worst-case scenario, it minimizes the possible loss. On the other hand, the gaining scenario maximizes the minimum gain. 

• The time complexity of Mini-Max is O(n^m)
• The space complexity of Mini-Max is O(nm)

Where n is the number of optimal moves at each turn and m is the maximum depth of the tree.

Mathematical Expression for Mini-Max:

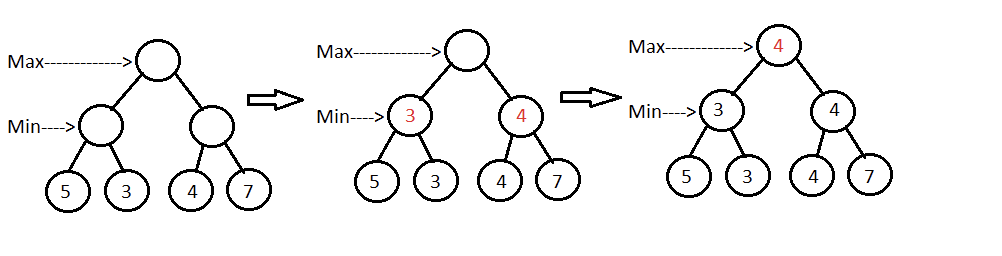
According to the above figure, we can analyze the operation of the mini-max algorithm. Here, maximize initiated with the root node and choose the solution with maximum weight. Whereas only leaf nodes have the weights, the algorithm should recursively reach the leaf nodes. The illustration of the above figure demonstrates that each level in the tree is alternatively portioned as min and max utilization. The min value of the rightmost leaf node is three, and similarly, the leftmost leaf node is 4. Further, the root node grabs the max weight between its child nodes which is 4. Therefore, it chooses the following path from the optimal solution arrived at the root node. We made evaluations based on the preferences and weights assigned in the program. However, the evaluation function validates on the result node. 

Mini-Max Algorithm:

According to the game theory, alpha-beta pruning is the enhancement version of mini-max. In precise, alpha-beta pruning is an adversarial search algorithm that eliminates the unnecessary nodes and branches that are evaluated by the mini-max algorithm. Alpha-Beta prunes away the nodes, which does not affect the final solution. Hence, this pruning technique evacuates most of the nodes, which reduces the compilation time.

• The best-case time complexity of Alpha-Beta Pruning is O(n^m/2)
• The worst-case time complexity of Alpha-Beta Pruning is like Mini-Max Algorithm which is O(n^m)
• The space complexity of Alpha-Beta Pruning is O(nm)

Where the constraint is α ≥ β 

n is the branching factor and m is the depth of the tree.

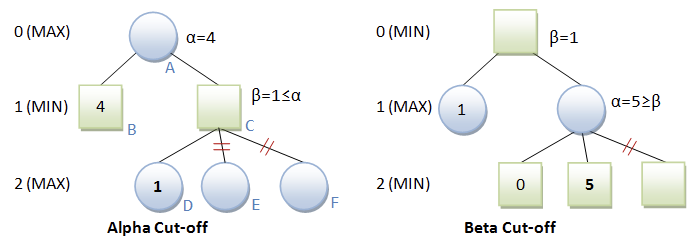
The above diagram illustrates the operation of Alpha-Beta pruning. Like the mini-max, each level of the tree is portioned as min or max alternatively. Further, alpha-beta checks whether the following leaf node or child node should be considered for further evaluation to obtain an optimal result. If not, the pruning happens right there. Here the terms alpha & beta represents the maximizing player and minimizing player, respectively. The above figure demonstrates that the leaf node gets only weight one because it is the minimum weight that reaches the min level in the tree.

Further, the root node accepts only the max value. Hence, the children of the leaf node can be eliminated except the child resultant to the node. This is similar for both the above mentioned figures, where α is for maximizing player and β is for minimizing player.

Alpha-Beta Algorithm:

Input:

The inputs of our project implementation are,

• User can choose the algorithm to play (Whether to play with mini-max or alpha-beta)
• User can choose the depth value

Output:

The outputs of our project implementation are,

• Game: User vs Mini-Max & User vs Alpha-Beta Pruning
• Compilation Time
• Output set for selected algorithm
• Space Allocation for selected algorithm 

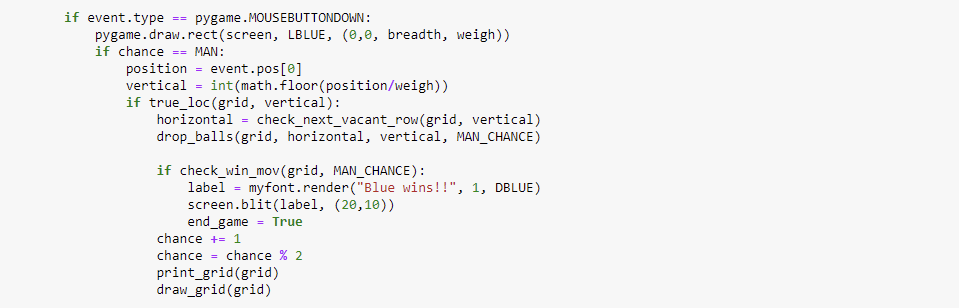
Game Output: User vs AI

Here, the AI move is white ball and User move is blue ball

Mini-Max Compilation Time & Output Set:

Alpha-Beta Compilation Time & Output Set:

From the above two outputs, we can analyze that the compilation time of alpha-beta was 7.786 milliseconds at depth 3, and at the same depth value, the compilation time of mini-max was 21.756 milliseconds, which demonstrates that alpha-beta utilizes half of the compilation time needed by mini-max, which justifies our statement that alpha-beta pruning is the better implementation to mini-max algorithm according to time complexity. 

Mini-Max Algorithm Space Allocation Output:

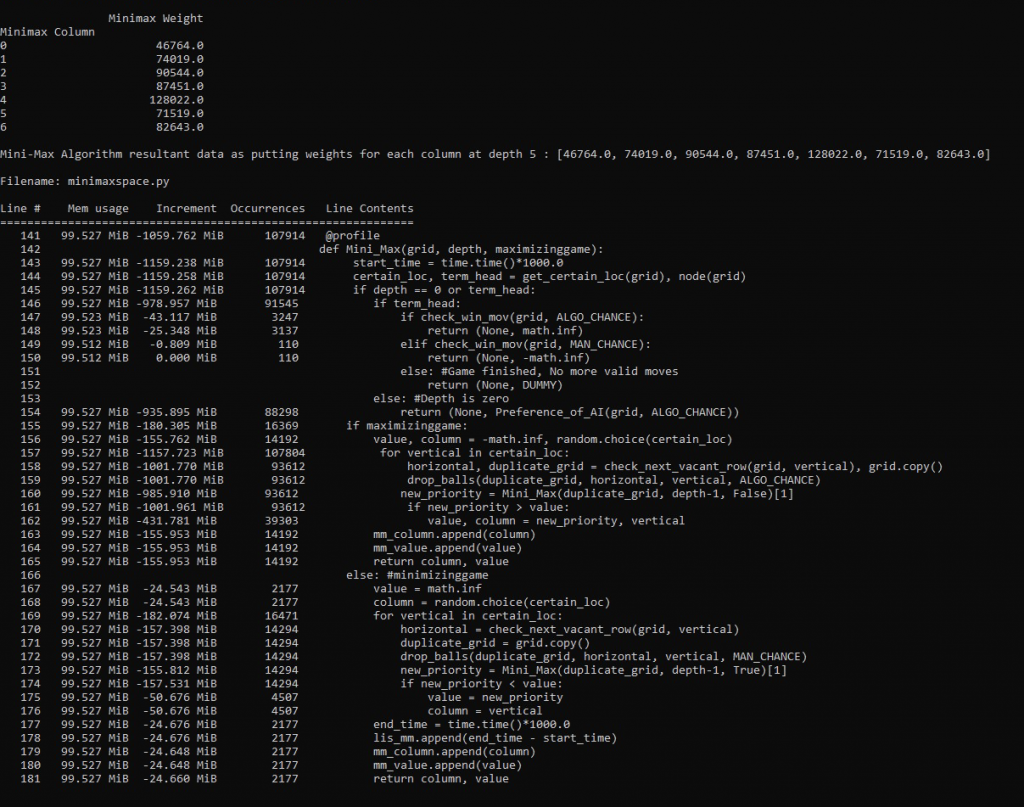
We used memory_profiler python module to gather space allocation data for specific algorithm (Function). Above figure is the space allocation output for mini-max function. As we can see that the memory usage of mini-max function was 99.527 mebibyte at depth 5 and the occurrences it makes was 107914 iterations.

Alpha-Beta Pruning Algorithm Space Allocation Output:

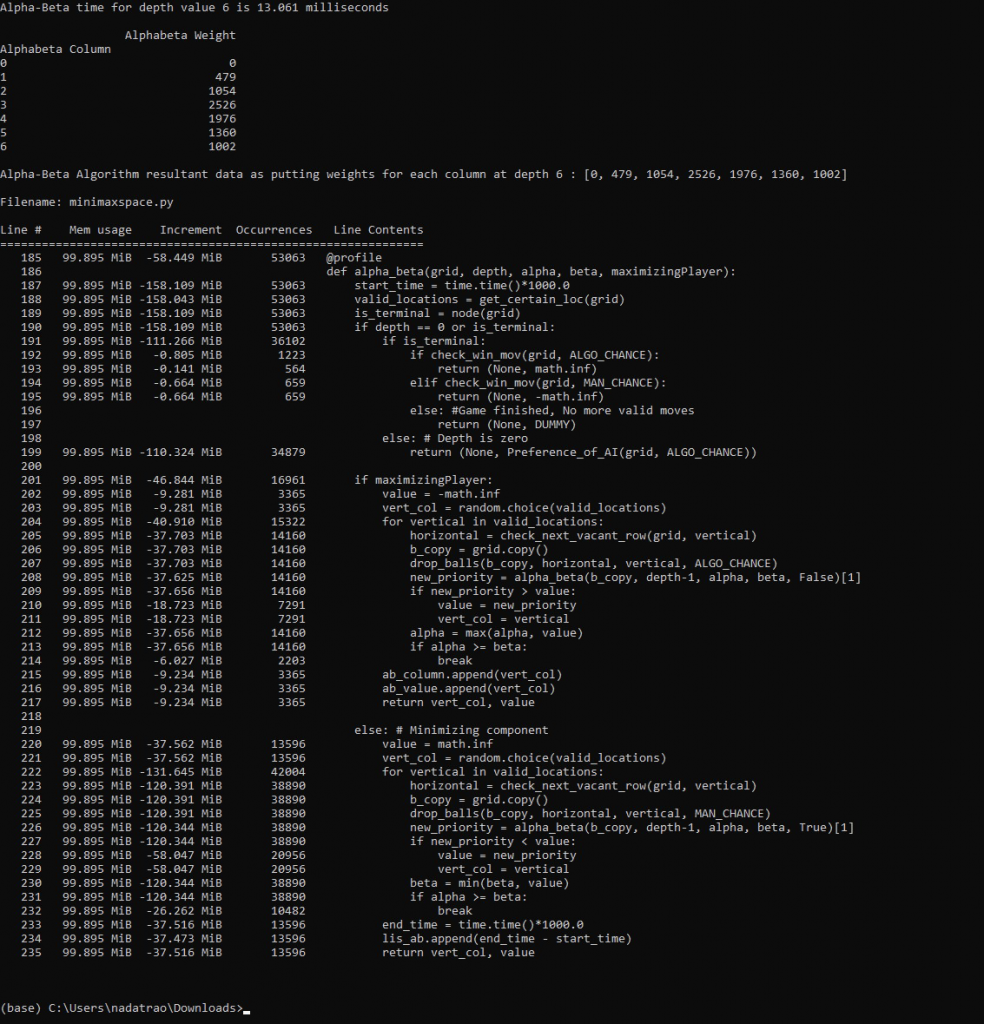
According to the memory_profiler python module “@profile,” the decorator provided the space allocation data for Alpha-Beta Algorithm (Function). As a result, the memory usage of the alpha-beta function in our program at depth 6 was 99.895 mebibyte, and the occurrences were 53063 iterations. 

The above two figures of space allocation data demonstrate that though the space allocation of both algorithms was almost similar, there is much difference between occurrences of iterations performed. Alpha-Beta pruning algorithm performed fewer iterations than mini-max. This justifies that the alpha-beta compiles in less time compared to mini-max.

We gathered the output set data for each algorithm at every depth value. Output set data is the data we get from the return stage of each function (either mini-max or alpha-beta). So, for example, the average weight that the algorithm dropped like a ball to fill in any 7 columns is gathered as an output set data. Further, we utilized this output data to calculate the accuracy of the performed algorithm.

We evaluated the performance of both the algorithms on three metrics they are,

• Compilation Time
• Space Allocation
• Accuracy

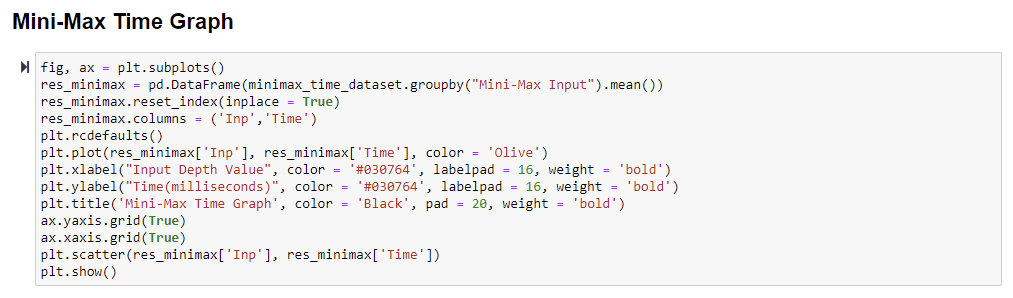
Compilation Time Graph of Mini-Max Algorithm:

We took 10 different samples of compilation time for every depth value ranges in mini-max from output. The highest depth value in mini max was 5 hence, we took 50 samples of compilation time data. According to the gathered compilation time data, we plotted a line graph by utilizing matplotlib python library. We took the line graph based on depth value as independent metrics (x-axis) and compilation time (milliseconds) as dependent metrics (y-axis).

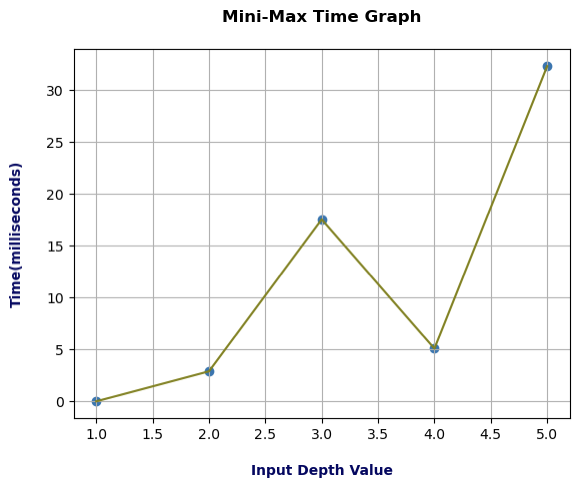
According to the above time graph of mini-max, we can analyze that though there are fluctuations in the graph, as the depth value increases, compilation time also increases. However, the compilation time at every even depth value decreases because the balancing in the tree happens there. The highest compilation time was recorded at the maximum depth value of mini max, above 30 milliseconds. The second highest compilation time was around 17 milliseconds. The compilation time of mini-max at even depths is below 5 milliseconds at depth 2 and 5 milliseconds at depth 4. 

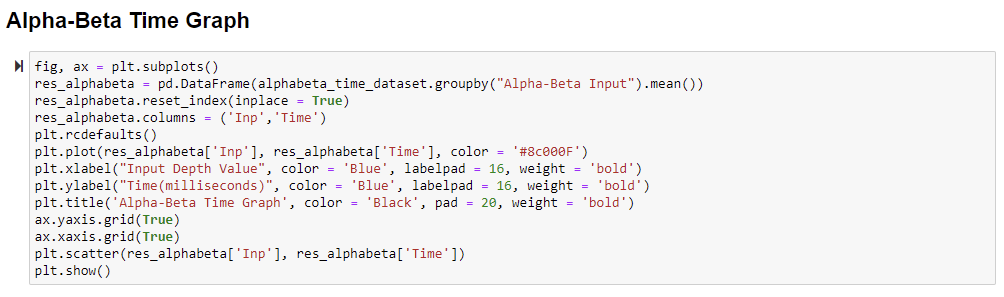
Compilation Time Graph of Alpha-Beta Pruning Algorithm:

We took 10 different samples of compilation time for every depth value range in alpha-beta from the output. The highest depth value in alpha-beta was 8. Hence, we took 80 samples of compilation time data. According to the gathered compilation time data, we plotted a line graph by utilizing the matplotlib python library. We took the line graph based on depth value as independent metrics (x-axis) and compilation time (milliseconds) as dependent metrics (y-axis).

According to the below time graph of alpha-beta, we can analyze that even though the line graph fluctuates, the variations are not very massive compared to mini-max variations. The alpha-Beta pruning algorithm also recorded less compilation time at even depth values. We previously said that alpha-beta does not provide a different solution than mini-max, which specifies that alpha-beta was also optimizing the almost same tree done by mini-max. 

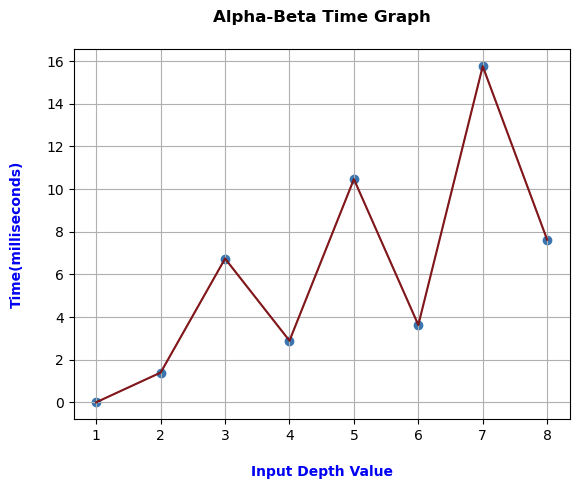
The highest compilation time recorded in alpha-beta time graph was 16 milliseconds at depth 7. However, alpha-beta highest depth value is 8 with below 8 milliseconds of compilation time. Moreover, the compilation time highly increases for every odd depth value for instance, at 3 it is over 6ms, at 5 it is over 10ms. And for even depth values there is slight increase i.e., at 4 it is around 3ms, at 6 it is under 4ms.

Compilation Time Comparison:

We plotted mini-max & alpha-beta time graphs on a single plot to get the comparisons visually. The below graph demonstrates the considerable variation of compilation time between mini-max and alpha-beta. Here, in the plot, mini-max was furnished with olive green color, and at the same time, alpha-beta was furnished with maroon color. Moreover, the dependent and independent axes are time in milliseconds and input depth values.

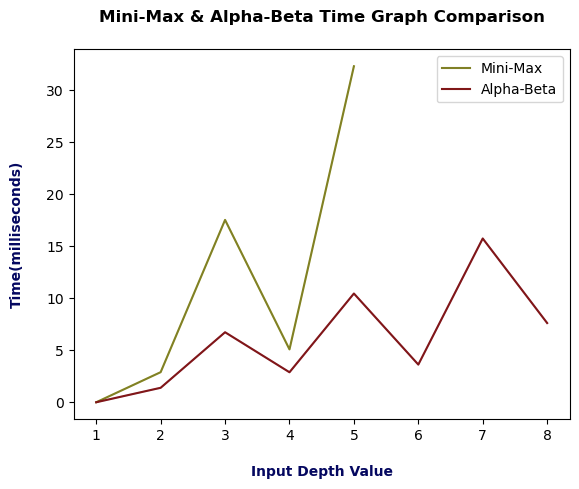
We can clearly distinguish the algorithm’s compilation time from the graph above. The output was stopped at depth 5 in mini-max, but in alpha-beta, it continues till depth 8. The highest compilation time of mini-max was double the maximum compilation time demonstrated by alpha-beta at every depth value except depth 1. The compilation time at depth 3 was around 17 milliseconds in mini-max, but at the same depth, alpha-beta was around 6 milliseconds. A similar point in both the algorithms was less time complexity at even depths which happens because of the balancing in the tree at even depths. However, the even depths compilation time of alpha-beta is less than mini-max. For instance, at depth 4, the mini-max time taken was 5 milliseconds, but alpha-beta reduced it to around 3 milliseconds. We can observe that the compilation time of alpha-beta is half of mini-max at every depth value. This means that the alpha-beta pruning search can search twice as profoundly within the same amount of time. 

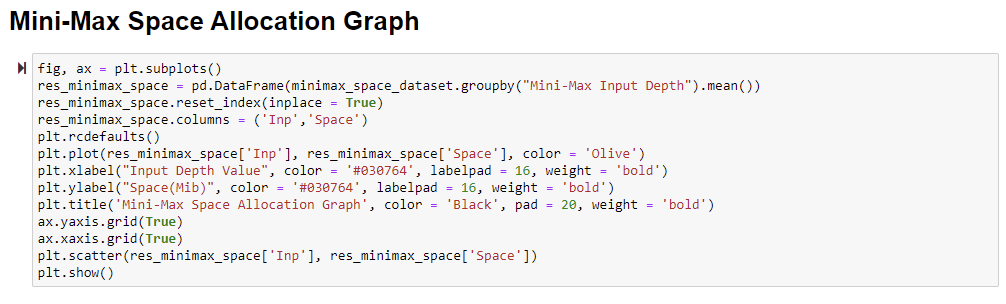
Space Allocation Graph of Mini-Max Algorithm:

We gathered 10 samples of space allocation (memory usage) data at every depth value for both the functions (mini-max function or alpha-beta function) as preferred by the user. 50 rows of space allocation sample data and 2 columns which are input depth column and space allocation (memory usage). We plotted the space allocation line graph of mini-max where the independent (x-axis) metrics and dependent (y-axis) metrics was input depth value and space allocation in Mebibyte, respectively. 

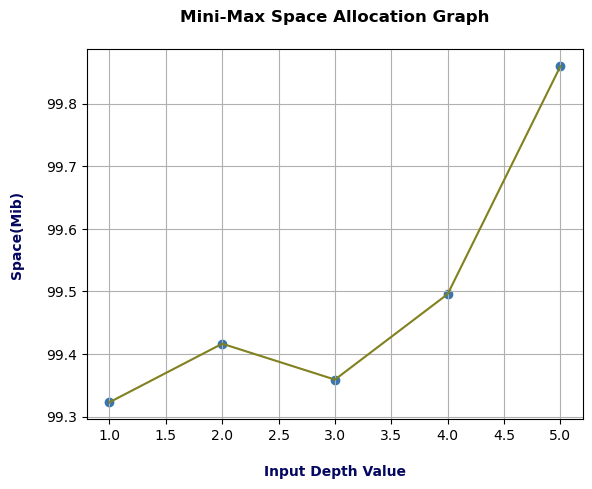
From the above mini-max space allocation line graph, we can analyze that as the depth value increases, the space utilization and space complexity increase. At the same time, we can compare this space graph with the time graph of mini-max so that we can assimilate that at depth 3, the compilation time increases, but at depth 3 the space allocation decreases. Moreover, at depths 2 and 4, the space complexity was reduced compared to the time complexity graph of mini-max. This concludes that as time complexity increases, space complexity decreases and vice-versa. The space allocation at depth 2 was over 99.4 Mib, at depth 3 was below 99.4 Mib, and at depth 4 was exactly 99.5 Mib. However, at depth 1 and depth 5 there is a slightly different recording to our analysis. This happens because depth 1 is the initial parameter which does not influence preference weightage. Hence, at depth 1 there is a fluctuation in space allocation as it depends on the user performance. Subsequently, at depth 5 there is a high increase in space allocation as it is the highest depth level in mini-max. The algorithm must perform its operation for every node in the tree with recursive occurrences to the leaf node. Hence, the space allocation at depth 5 is enormous.

Space Allocation Graph of Alpha-Beta Pruning Algorithm:

We gathered 10 samples of space allocation (memory usage) data at every depth value for the alpha-beta function. 80 rows of space allocation sample data and 2 columns which are input depth column and space allocation (memory usage). We plotted the space allocation line graph of alpha-beta where the independent (x-axis) metrics and dependent (y-axis) metrics was input depth value and space allocation in Mebibyte, respectively. 

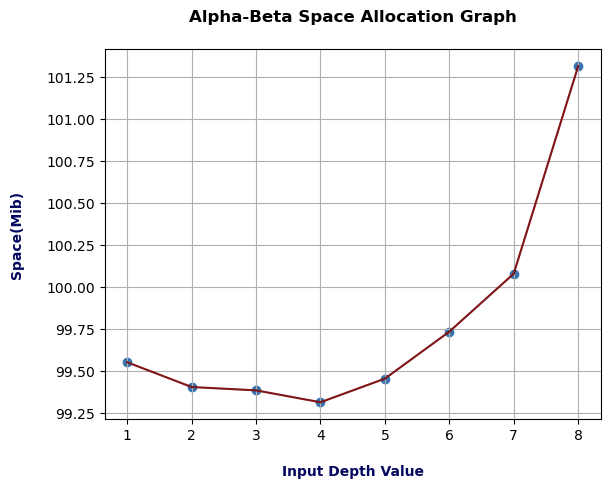
According to the above space allocation graph of alpha-beta, we can observe that as the depth value increases, the space complexity also increases. The space allocation varies between 99.30 Mib and 101.30 Mib for depth 1 to depth 8. The height space allocated at depth 8, which was 101.30 Mib. Later, at depth 7 there is a drastic decrease in the space utilization, around 100 Mib. Further, it reduces and is recorded as 99.3 Mib at depth 4. There were slight fluctuations of space allocation at depth 2 and depth 3, which were recorded as almost the same, i.e., 99.35 Mib.

Comparison Space Allocation Graph:

We plotted mini-max & alpha-beta space graphs on a single plot to get the comparisons visually. The below graph demonstrates almost similar space allocation between mini-max and alpha-beta. Here, in the plot, mini-max was furnished with olive green color, and at the same time, alpha-beta was furnished with maroon color. Moreover, the dependent and independent axes are space in mebibytes and input depth values.

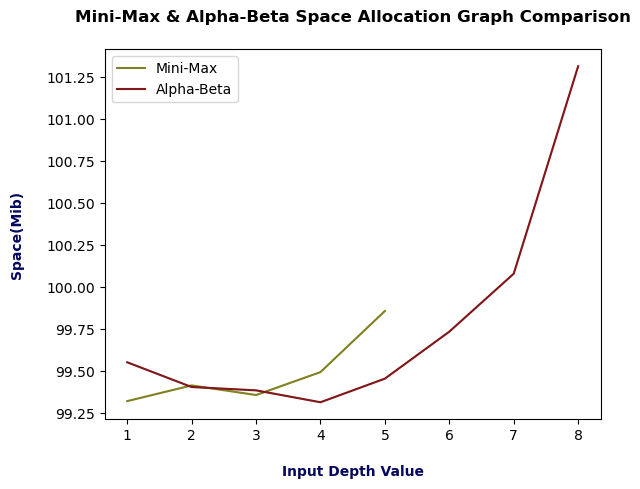
The above space comparison graph shows that both algorithms utilize almost the same space or memory usage. However, there is a considerable difference in occurrences or iterations performed between both the algorithms. In both algorithms, as depth value increases, space allocation also increases. In concise comparison, we can conclude that compared to the mini-max algorithm alpha-beta pruning algorithm utilizes less space allocation. For instance, we can figure that at depth 4 and depth 5, alpha-beta occupied 99.3 Mib and 99.50 Mib, respectively. However, on the other hand, at the same depths, mini-max occupied over 99.50 Mib and 99.85 Mib, respectively. Later, alpha-beta continued, and mini-max performance ended at depth 5. 

The observation at depth 1 for both the algorithms is different. As depth 1 is the initial depth value in both the algorithms, which does not have much significance in performing the weightage model of AI. Because it is the most accessible level where users have the chance of winning, though the compilation time of both the algorithms was the same at depth 1, there is a slight difference in space allocation. At depth 1 the mini-max and alpha-beta space allocation was recorded as 99.3 Mib and 99.6 Mib, respectively. This happens because depth 1 of alpha-beta comes under the worst-case scenario, which does not calculate based on the user’s movement or winning optimal predicted move. It was just a random decision-making move in which performance in a minor concern. Hence, mini-max was calculating and storing the min and max values of the tree. Nevertheless, alpha-beta calculates and stores the maximizing player move and minimizing player move and stores the data eliminated in the pruning method. In conclusion, alpha-beta stores more data at depth 1 compared to mini-max.

Accuracy of Mini-Max & Alpha-Beta Pruning Algorithm:

We gathered the 10 output set samples for every depth value of the mini-max & alpha-beta pruning algorithm. The mini-max accuracy data consists of 50 rows and 8 columns, and the alpha-beta accuracy data consists of 80 rows and 8 columns. The gathered data represents the output weight to its correspondent column respective to its input depth value. According to the sklearn python module, we pre-processed the data and further divided the data into two sets: the training set and the testing set. Furthermore, we made the test size equal to 0.25, which was quarter data is processed for testing. Later, we transformed and fitted data subsequently between training and testing data. To calculate the accuracy score performed by the data, we have implemented Logistic Regression on the pre-processed data. Logistic Regression is an ML model based on a statistical analysis method to predict a binary outcome, likely True or False, on prior observations and calculations. The Logistic Regression model predicts dependent metrics by assimilating the relationship between one or more independent metrics.

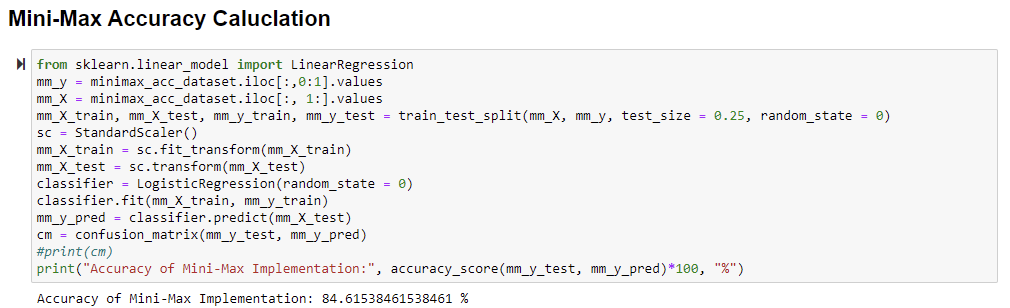
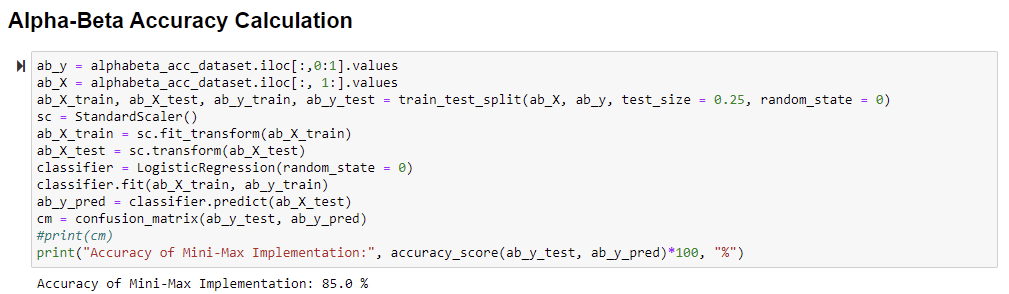
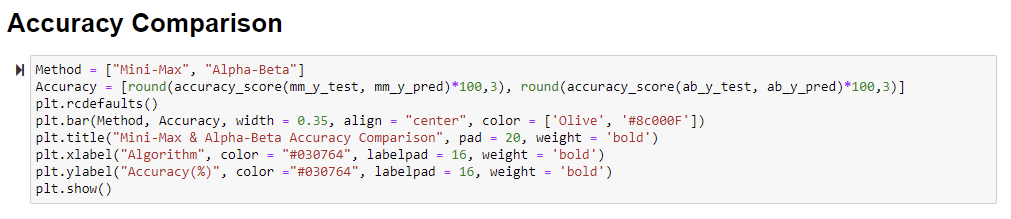
• The accuracy of Mini-Max Algorithm was 84.61%
• The accuracy of Alpha-Beta Algorithm was 85%

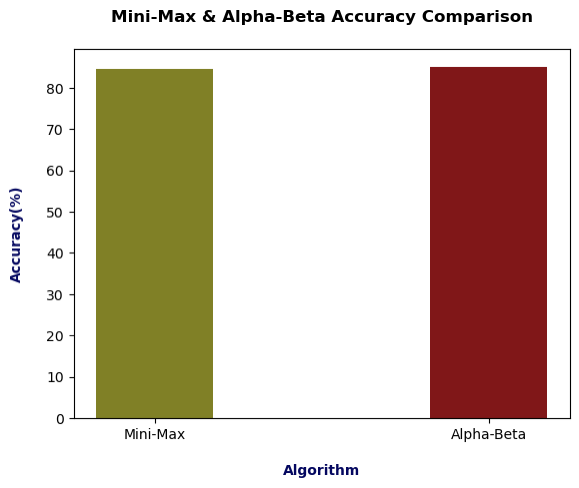
The accuracy of both algorithms is almost the same. However, the accuracy of alpha-beta is slightly more compared to mini-max. In conclusion, both algorithms give the same solution or move prediction or accuracy. However, the crucial difference is that alpha-beta does not explore all the paths, unlike the mini-max algorithm. Therefore, the alpha-Beta pruning algorithm eliminates those guaranteed not to be an optimal solution for the spot. Therefore, the alpha-beta pruning algorithm is a better implementation than the mini-max algorithm. 

Program: https://github.com/krishnaAdatrao/Connect4Game.git

## Python Modules & Libraries

We utilized the built-in modules of python likely, NumPy, for building matrix calculations, Pandas for data processing and building datasets, and Math library for mathematical calculations used in the program. For visual effects and game structural graphics, we used the pygame module. Seaborn and Matplotlib libraries were used for plotting visual graphs. Sklearn module is scikit learn for machine learning library, consisting of various likely methods, classification, regression, and clustering algorithms. We utilized the classification process from the sklearn module, divided our return data into testing and training sets, and applied logistic regression from the sklearn module to the data-driven to calculate accuracy. 

# Connect4 Program Implementation using Mini-Max Algorithm & Alpha-Beta Pruning Algorithm 

## Input & Global Variables

## Board Creation

## Function to strike 4 (Game Concept)

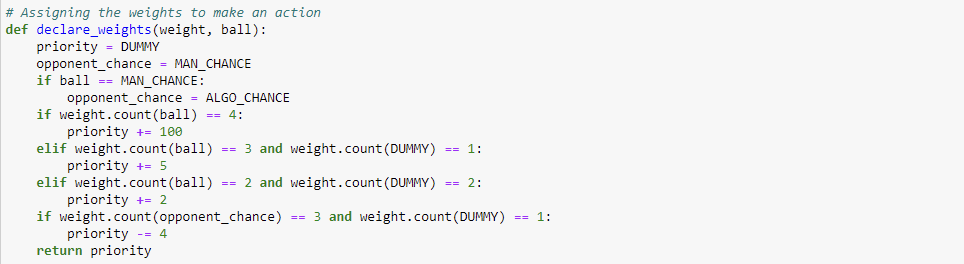
## Assigning Weights

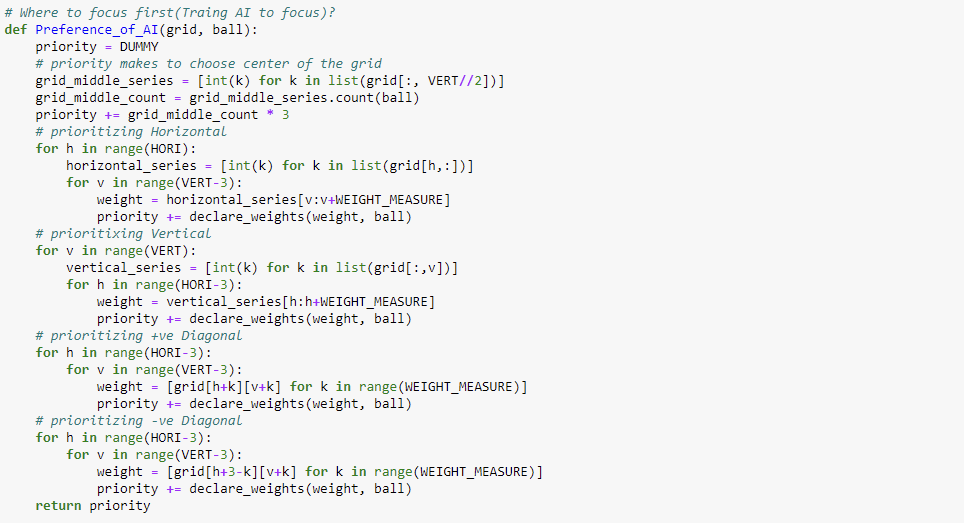
## System Preference of dropping pieces while playing

## Terminal Node Function

We have defined a function certainly works on checking the status of terminal node in the tree. The function was applied as a condition in mini-max algorithm.

According to our monitor aspect ratio, we gave fixed size of the board with 6 rows and 7 columns at Board Creation

The independent functions used in implementing mini-max or alpha-beta are almost same for both the algorithms (mini-max algorithm & alpha-beta pruning algorithm). 

Bench-mark Function – Implementation of Mini-Max Algorithm

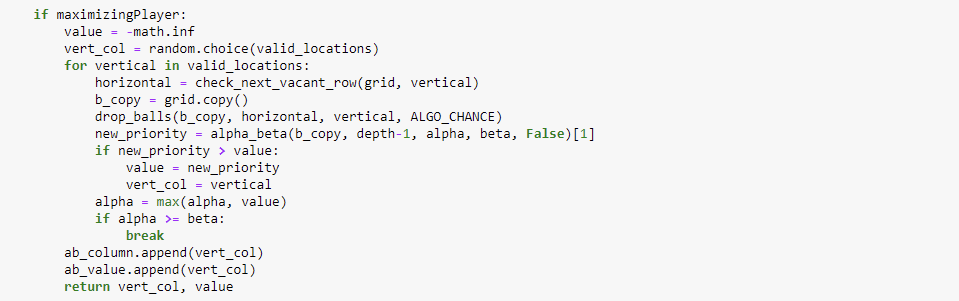
Optimal or Proposed Function – Implementation of Alpha-Beta Pruning Algorithm

# Implementation of Mini-Max Algorithm Function

# Implementation of Alpha-Beta Pruning Algorithm Function

## Priority Selection Function

## Updating Board

## Variables Declaration

## Logic Implementation

## Output

# Program for Performance Evaluation Metrics

## 1. Compilation Time Comparison

## 2. Space Allocation Comparison

## Accuracy Comparison

None of the milestones are remaining. We learned the operation of how the mini-max algorithm and alpha-beta pruning algorithm works? As mini-max is exploring all the paths to get the optimal move, on the other hand, alpha-beta is eliminating some of the trees, which is unnecessary, and removal does not affect the optimal solution as well. Further, the adversarial search made by alpha-beta to get an optimal solution is in half of the time of mini-max. Moreover, we got a clear understanding between time complexity and space complexity. How are they related to each other? As time varies, space varies, either mutual or contrast. In our program, as time complexity increases, space complexity decreases and vice-versa. Finally, the adversarial search makes the prediction faster with sustainable accuracy.

In conclusion, while we have gone deeper into the depth of mini-max, the output has been taking a considerable time. Because the mini-max algorithm’s time complexity is O(nm), it has been checking for an optimal move by going to the very last level in the tree recursively. To solve this, we considered alpha-beta pruning upon mini-max to quickly achieve an output by testing the same depth levels of a tree. This has been happening because the alpha-beta algorithm certainly checks for the optimal branch to make a move while removing the irrelevant branches by checking the weight of each node on maximizing and minimizing concepts. Hence, it has O(nm/2) time complexity which resembles that it has been cutting lots of the tree and getting the same solution as mini-max in half the amount of time. So, alpha-beta is a better implementation of mini-max. Our future work is to enhance alpha-beta implementation by deep-pruning & iterative-deepening techniques. Iterative Deepening DFS Search, in which a depth-limited version of DFS repeatedly runs with adding depth value until the solution is found. We proposed iterative deepening for reducing space complexity. This technique utilizes less space or memory allocation. Because iterative-deepening search operates in the same order, DFS does, but BFS happens in the cumulative order in which nodes are first visited. The space complexity of iterative deepening search is O(d), where d is the depth of the solution.

• Ana Carolina Ribeiro, Luis Miguel Rios and Ricardo Meneses Gomes “Data mining in adversarial search — player’s movement prediction in connect 4 games” 2017 12th Iberian Conference on Information Systems and Technologies (CISTI).
• SaminehBagheri, Markus Thill, Patrick Koch and Wolfgang Konen “Online Adaptable Learning Rates for the Game Connect-4” IEEE Transactions on Computational Intelligence and AI in Games.
• Simon M. Lucas and Thomas Philip Runarsson “On imitating Connect-4 game trajectories using an approximate n-tuple evaluation function” 2015 IEEE Conference on Computational Intelligence and Games(CIG).
• I. Levner, A. Kovarsky and Hong Zhang “Heuristic search for coordinating robot agents in adversarial domains” Proceedings 2006 IEEE International Conference on Robotics and Automation, 2006. ICRA 2006.
• Xiyu Kang1*, Yiqi Wang2*, Yanrui Hu3*, “Research on Different Heuristics for MinimaxAlgorithm Insight from Connect-4 Game” Journal of Intelligent Learning Systems and Applications, 2019, 11, 15-31.
• “Mini-Max Algorithm.” Wikipedia, Wikimedia Foundation, 12^th March 2022, en.wikipedia.org/wiki/Minimax.
• “Alpha-Beta Pruning.” Wikipedia, Wikimedia Foundation, 5^th March 2022, en.wikipedia.org/wiki/Alpha%E2%80%93beta_pruning.